Conway多項式を使って有限体の表現を一意に定めよう
有限体を生成する既約多項式の選択
前回の記事では有限体の代数的閉包について調べた。その際、有限体の間の包含関係には、包含のさせ方が一意に定まらないという問題があることを述べた。その具体例としてという単射が一意に定まらないということを確かめた。
しかし、よく考えるとこれはあまり大した問題ではないのかもしれない。というのも、結局とするか
とするかだけの問題であり、行き先となる集合は変わらないからである。
ただし、ここでは1つ暗黙的に固定しているパラメータがあった。それは既約多項式の選択である。既約多項式として他のものを選べば具体的な集合の要素は変わってくる。もちろんどのような既約多項式で商体を作ろうが結果は全て同型ではあるのだが、具体的な表現の仕方が異なる。何か数学的に自然な既約多項式の選択方法はないものだろうか?
本稿ではこの問題を解決するアプローチの1つとして、Conway多項式を用いる方法を紹介する。ガッカリされないように先に述べておくと、既約多項式として数学的に自然なものをただ1つ選ぶようなうまいやり方はない。そんな中でも、多少なりともcanonical感のある選択をしようという話である。
注意
Conway多項式というのはどうやら複数の概念を表す言葉らしく、Wikipediaに曖昧さ回避のページがある[1]。本稿で言うところのConway多項式とは有限体に関するものであるため注意されたい。
Conway多項式
定義
Sageのドキュメントに書いてある定義が分かりやすいので引用する[2]。
is irreducible.
- In the quotient field
, the element
generates the multiplicative group.
- The minimal polynomial of
equals the Conway polynomial
, for every divisor
of
.
is lexicographically least among all such polynomials, under a certain ordering.
これだけ見ると、最後の"lexicographically least"というところが良く分からない。これはWIkipediaの方の定義を見ると分かる[3]。
- The elements of
are ordered
.
- A polynomial of degree
in
is written
and then expressed as the word
. Two polynomials of degree
are ordered according to the lexicographical ordering of their corresponding words.
こちらの定義を見るとlexicographical orderingを具体的にどのように定めているかが分かる。逆に"compatible with for all
dividing
"というところが(私の引用の仕方の都合で)分かりづらいが、これは要するにSage版の定義に出てくる3つ目の条件を満たす必要があるということである。
また、は
を割り切る正の整数として定められているように見えるが、それで言うと
として
自身も許されるはずである。しかし、それだとSage版定義の条件3にて再帰的に
がConway多項式であることを確かめようとしているときに、
自身がConway多項式であることが必要になるという意味不明な状況になる。そう考えると、恐らく暗黙的に
が仮定されているのではないかと推測される。
Wikipedia版の定義ではConway多項式は原始多項式 (primitive polynomial) であると明記されているが、Sage版にはその記載がない。しかし、Sage版定義の条件2がそのまんま原始多項式であるための条件なので、同じことである。
辞書順で何かを選択するということ
前述のSage版定義の条件4では候補となる多項式を辞書順に並べて順序が最小となるものを選択している。これは非常に苦しい。というのも辞書順をどうやって決めるかというのは恣意性があり、数学的な構造から自然に決まるものではないからである。極端な話、順序を逆にしてもよいわけである。
辞書順で何かを選ぼうというのは、こういうcanonicalでない選択を迫られた時の苦肉の策として使うものなのだろう。
辞書順を決める際の各項の符号について
辞書順を定める際に各項の符号が正負交互になっているが、これはなぜだろうか?明確な理由は書かれていないので私の想像になるが、これはいわゆる「解と係数の関係」の式に関連していそうな気がしている。例えば以下のように1次式の積に分解された3次多項式があったとする。
これを展開すると以下のように各項の符号が正負交互になっているような多項式が現れる。
推測で物を言っているので何も証拠はないのだが、文脈によってはこちらの形式を好む人がいるのも分かるような気はする。
Conway多項式は常に存在するか?
Conway多項式は素晴らしいアイディアのように思えるが、果たしてこれは常に存在するのだろうか?つまり、任意の素数と1以上の整数
について
が定義されるのだろうか?これについてはみんな"Endliche Körper in dem gruppentheoretischen Programmsystem GAP"という同じ論文を引用しているようで、以下に本家らしきWebページがある。
https://www2.mathematik.tu-darmstadt.de/~nickel/information.shtml
しかし、残念なことにこちらからリンクされている論文の本体ファイルはリンク切れしているようで、結局論文を見つけることはできなかった。どなたか見かけたらTwitterでもブログコメントでもよいので教えて頂けるとありがたい。
 が整数であることの確認
が整数であることの確認
念のためが常に整数であることを確認しておこう。
を変形して整理すると以下のようになる。
ここで、は
を割り切るので、上式は以下のように変形できる。
以上によりは整数であることが分かった。
具体例で確認してみよう
例としてのケースでいくつかConway多項式を具体的に求めてみよう。
上の1次多項式は
,
のいずれかであり、いずれも自明に既約である。ただし、原始多項式になっているのは
のみである。1より小さい正の整数はないのでSageの条件3はスキップできる。また、今は候補となっている多項式が
のみなので条件4もクリアできる。
以上によりである。
なお、Sage版の定義における条件4で辞書順に並び替えるときの形式に従うために、本当は符号を交互にすべきである。しかし、標数2であれば符号はどちらでもよいし、単に私が混乱するので全ての項の符号は正としておく。
上の2次既約多項式は
のみである。これが原始多項式であることを確かめるために、Sage版の定義に従って商体
において
が乗法群を生成することを直接的に確認してみよう。
ということで確かに乗法群を生成することが分かった。
Sage版定義の条件3について、の取り得る値は1のみである。このとき
は以下のようになる。
1の最小多項式はなので、確かに
と一致している。
最後に辞書順で一番小さいものを選べば良いわけだが、今回は候補が1つしかないのでこのステップはスキップできる。
以上により、であることが分かった。
上の3次既約多項式は
,
の2つである。まずはこれらが原始多項式であることを確かめたいが、愚直にやるのは面倒になったのでSageで確認してみる。
sage: R = PolynomialRing(GF(2),'x') sage: x = R.gen() sage: (x^3 + x + 1).is_primitive() True sage: (x^3 + x^2 + 1).is_primitive() True
ということでいずれも原始多項式であることが分かった。
Sage版定義の条件3について、の取り得る値は1のみである。このとき
は以下のようになる。
1の最小多項式はなので、確かに
と一致している。
また、は以下のようになる。
これも先ほどと同様に最小多項式がと一致している。
というわけで、今回は辞書順に並べて最小のものを選ぶ必要がある。の方が順序が小さいので、結局
となる。
上の4次既約多項式は
,
,
の3つである。まずはSageを使ってこれらが原始多項式かどうか確かめる。
sage: R = PolynomialRing(GF(2),'x') sage: x = R.gen() sage: (x^4 + x + 1).is_primitive() True sage: (x^4 + x^3 + 1).is_primitive() True sage: (x^4 + x^3 + x^2 + x + 1).is_primitive() False
ということで,
は原始多項式であることが分かった。
Sage版定義の条件3について、の取り得る値として今回は1, 2の2つがある。
のケースを計算してみて分かったが、
のときは
となるため、
が原始根であることより
(
はConway多項式の候補となる多項式) の値は必ず1になる。1の最小多項式は
なので、
については条件を満たす。
のケースについて、まずは
が条件3を満たすか確かめてみる。
このときは以下のようになる。
の最小多項式は(ややこしいので変数を
とすると)
となる。具体的に
上で因数分解すると
となる。これは
に等しいので条件を満たす。
次にが条件3を満たすか確かめてみる。
このときは以下のようになる。
の最小多項式は(やはり変数を
とすると)
となる。具体的に
上で因数分解すると
となる。これは
に等しいので条件を満たす。
というわけで、今回は辞書順に並べて最小のものを選ぶ必要がある。の方が順序が小さいので、結局
となる。
Sageによる確認
以上、いくつか具体例を計算してみたが、ぶっちゃけこれ本当に合っているのか?という気持ちは拭えない。というわけでSageでも計算してみた。
sage: from sage.rings.finite_rings.conway_polynomials import PseudoConwayLattice sage: PCL = PseudoConwayLattice(2, use_database=True) sage: PCL.polynomial(1) x + 1 sage: PCL.polynomial(2) x^2 + x + 1 sage: PCL.polynomial(3) x^3 + x + 1 sage: PCL.polynomial(4) x^4 + x + 1
計算方法はSageのドキュメント[2]を参照しつつ、use_databaseオプションだけTrueにした。これは実際にConway多項式を計算するのではなく、Sage内部に持っているデータベースを使用するというオプションである。
詳細は後述するが、SageでConway多項式を計算するときは、本物のConway多項式ではなくpseudo Conway polynomialというものを計算しているらしい。一方、データベースを使用する場合は本物を返してくれるようにドキュメントから読み取れる。次数が4くらいまでであればデータベースに入っているだろうと想定して、ここではuse_databaseをTrueにした。
まあ細かいことはさておき、私が具体例のところで出した結果と一致することが分かった。
Sageが持つConway多項式のデータベースを直接確認しよう
※この章は数学的な学びは全くないので読み飛ばしても構わない。
「次数が4くらいまでであればデータベースに入っているだろう」と言ってはみたが、「本当に?」と問われると反論できないので、念のためSageのソースコードを確認した。どうやらデータベースの実体はconway_polynomials.pという不思議な拡張子のファイルらしい。
https://github.com/sagemath/sage/blob/9.8/src/sage/features/databases.py#L39
locateコマンドでファイルパスを突き止めて中身を見てみたが、どうもバイナリファイルになっているようで内容の解釈ができなかった。
$ hexdump -n 128 -C /usr/share/sagemath/conway_polynomials/conway_polynomials.p 00000000 80 02 7d 71 00 28 4b 02 7d 71 01 28 4b 01 4b 01 |..}q.(K.}q.(K.K.| 00000010 4b 01 86 71 02 4b 02 4b 01 4b 01 4b 01 87 71 03 |K..q.K.K.K.K..q.| 00000020 4b 03 28 4b 01 4b 01 4b 00 4b 01 74 71 04 4b 04 |K.(K.K.K.K.tq.K.| 00000030 28 4b 01 4b 01 4b 00 4b 00 4b 01 74 71 05 4b 05 |(K.K.K.K.K.tq.K.| 00000040 28 4b 01 4b 00 4b 01 4b 00 4b 00 4b 01 74 71 06 |(K.K.K.K.K.K.tq.| 00000050 4b 06 28 4b 01 4b 01 4b 00 4b 01 4b 01 4b 00 4b |K.(K.K.K.K.K.K.K| 00000060 01 74 71 07 4b 07 28 4b 01 4b 01 4b 00 4b 00 4b |.tq.K.(K.K.K.K.K| 00000070 00 4b 00 4b 00 4b 01 74 71 08 4b 08 28 4b 01 4b |.K.K.K.tq.K.(K.K| 00000080
仕方がないのでプログラムからデータベースの中を覗いてみることにした。ソースコードの以下のあたりを読んで、実際に登録されているデータベースの情報を引っ張りだしてみた。
https://github.com/sagemath/sage/blob/9.8/src/sage/databases/conway.py#L179-L210
sage: C = sage.databases.conway.ConwayPolynomials() sage: C.polynomial(2, 1) (1, 1) sage: C.polynomial(2, 2) (1, 1, 1) sage: C.polynomial(2, 3) (1, 1, 0, 1) sage: C.polynomial(2, 4) (1, 1, 0, 0, 1)
出力に出てくる数字は左から順に0次の項、1次の項・・・という風に解釈すればよい。なお、データベースに存在しないものを取得しようとすると以下のようにRuntimeErrorになる。
sage: C.polynomial(2, 1000) --------------------------------------------------------------------------- KeyError Traceback (most recent call last) /usr/lib/python3/dist-packages/sage/databases/conway.py in polynomial(self, p, n) 221 try: --> 222 return self[p, n] 223 except KeyError: ・・・長いので割愛・・・ RuntimeError: Conway polynomial over F_2 of degree 1000 not in database.
もしくはドキュメントに書かれている以下の関数を使ってもデータベースへの登録状況が分かるようだ。結果がbool型で得られるので、実用上はこちらの関数の方が使い勝手が良いだろう。
https://doc.sagemath.org/html/en/reference/finite_rings/sage/rings/finite_rings/conway_polynomials.html#sage.rings.finite_rings.conway_polynomials.exists_conway_polynomial
いずれにせよ、標数2の場合は少なくとも4次のConway多項式まではSageのデータベースに登録されていることが分かった。
Conway多項式を用いた有限体の表現
さて、話が発散しかかったが、結局言いたかったのは有限体を生成する際に使用する既約多項式としてはConway多項式を使えばよいということである。例としておよびその部分体
がどのように表現されるかを考えてみよう。
まず、を用いて
を
として表現する。
は4次原始多項式なので、その根は
を生成する。Conway多項式の性質より
は
の根であり、これも原始多項式なので
を生成する。つまり、
が
と同型になる。
は
に対応させればよい。これにより、
が具体的に表現されるのに加えて、部分体である
の表現も具体的に決まることが分かる。
Pseudo Conway polynomial
Sageのドキュメントを見ると、どうやらSageでは辞書順の条件は諦めているらしい。正確な理由は分からないが、恐らく全ての候補を見つけて辞書順に並び替えるという操作の計算量が大きくなるのを嫌ったのではないかと推測している。Sageではこの辞書順の条件のみを外したConway多項式もどきのことをpseudo Conway polynomialと呼んでいるようだ[2]。
試しにuse_database=Falseとしてpseudo Conway polynomialを計算してみると、4次多項式についてはSage版定義の条件1~3までで選ばれた他の多項式が出力された。
sage: from sage.rings.finite_rings.conway_polynomials import PseudoConwayLattice sage: PCL = PseudoConwayLattice(2, use_database=False) sage: PCL.polynomial(3) x^3 + x + 1 sage: PCL.polynomial(4) x^4 + x^3 + 1
有限体の代数的閉包
はじめに
有限体の代数的閉包ってどうなるんだろう?ずっと前にこの疑問を抱いてからずいぶんと時間が経ってしまった。どうにも最近は子どもとマイクラする時間が長すぎて趣味の時間が取りづらい。子どもが大きくなればそのうち親離れしてくのだろうか。今は時間がなくて苦しいが、未来のことを考えると寂しくなるのでやめておく。
さしあたっては、いつまでも疑問を寝かせておくと解決する情熱がなくなってしまうので、そろそろ重い腰を上げてこの課題に取り組んでみようと思う。
有限体の代数的閉包
出発点
以前の記事にも書いたように、有限体は代数的閉体にはならない。というわけで、有限体の代数的閉包は無限体になる。具体的にはどのような体になるのだろうか?
Wikipediaによると、どうやら以下のようになるらしい[1]。
この「体のコピー」という何とも言えない煮え切らない言い方は何なんだろうか・・・というわけでもう少し調べたところ、Mathematics Stack Exchangeに以下のような書き込みを見つけた[2]。
Given finite fields
and
with
then the compositum is the finite field
. This allows us to define the algebraic closure of
as the union
まだ「体のコピー」というのが何を言おうとしているのかは分からないが、とにかくの和集合を無限に取っていけば標数
の有限体の代数的閉包が得られるということは分かった。
ただ、主張の前半のcompositumがどうとかいうところは何を言わんとしているのかいまいち分からない。いや、と
の合成体(the compositum)が
だという直接的な主張は分かるのだが、「それが何か?」という感じである。果たしてこの人は何を言おうとしているのか?これについては後述する。
有限体の包含関係に関する微妙な問題
さらに調べるとYahoo知恵袋に面白い書き込みを見つけた[3]。
実は、その主張の意味、正確にいうとその和集合の意味はwell-definedではありません。(中略)おそらく、Wikipediaの「代数的閉包」のページから引っ張って来たのだと推測しています。Wikipediaのそのページに書いてある主張の方は意味が整合的に定義されており、かつ正しいです。そのページからの引用なら、主張を間違えていると言えるでしょう。
意味が整合的に定められていない、というのは、例えば、F_(2^2) ⊆ F_(2^4) ではない、ということです。例えば、2次及び4次の既約多項式を使って
F_4 = F_2[x]/(x^2+x+1)
F_16 = F_2[y]/(y^4+y+1)
と定義したとすると、集合として部分集合ではありません。
「単射準同型F_4→F_16が存在するのだから、それでもって同一視してやればいいじゃないか!」と思うかもしれませんが、F_4 → F_16は唯一ではありません。(中略)
つまり、
Aut(F_4)=Gal(F_4/F_2)
={id, (0→0,1→1,[x]→[x+1],[x+1]→[x])}
が単位群ではないせいで、F_4とF_16を別々に定義すると、F_4をF_16の部分集合として見なす標準的な方法が見つからず、和集合の意味が定義できない、ということなのです。
なるほど、和集合の定義がwell-definedにならないとは恐れ入った。Wikipediaで「体のコピー」というよく分からない言い方をしていたのは、このあたりの煩わしさを避けるためだったのではないかと思われる。
確かめてみよう
このことをもう少し深く理解するために、を
の部分集合として見なす標準的な方法がないということを自分でも確かめてみる。
まず、念のためと
が
上既約であることを確かめておこう。これはSageでサクッと確認できる(記号はなんでもよいでの両方ともxとした)。
sage: x=GF(2)['x'].gen() sage: (x^2+x+1).is_irreducible() True sage: (x^4+x+1).is_irreducible() True
とすると
は
に同型で、その元は
となる。また、
とすると
は
に同型で、その元は以下の16個である。
の部分集合
は
と同型である。これは愚直に計算すると分かる。
を
に埋め込む写像
のうち体同型になる可能性があるものとしては、
を
に写すような写像
と
に写す写像
の2つがある。
が体同型であるためには全単射でなければならないので、
,
である必要がある。これを仮定したときに、
について
,
が成り立っていることを確認できればよい。
についても同様である。
これは愚直に計算すれば分かる話なのだが、例として,
の和と積を
で写すケースについて確認しておこう。なお、以下では分かりやすさのために
における積の単位元をそれぞれ
と表記している。
・和をで写すケース
・積をで写すケース
他のケースも同様に計算していけば確かめられ、はともに体同型であることが分かる。というわけで、確かに
を
に埋め込む方法が一意に定まらないことが分かった。
で、どうすればいいのさ?
一意に定まらないならどうすればよいのか?と言うと、何らかの方法で一意に定めればよいということになる。要するに埋め込むための写像を1つ選べばよいわけである。その後の議論ではあまり選び方は重要ではなさそうなので深入りはしない。
有限体の包含関係に関する微妙な問題2
同様に、Mathematics Stack Exchangeに書かれていた合成体の下りについても、と
を含むような
を合成することで、
が
に含まれるかどうかを心配しなくて済むようにしていたのではないかと思われる。ただし、ここでは
を前提としており、
と
については話が成り立たない。
どうもこちらの投稿はとある論文[4]が元になっているようで、そちらを読んでみると素数に対して
は体の拡大列と捉えているようだ。拡大体を考えるにしても、部分体を考えるときのように拡大の仕方が複数あることに悩みそうな気もするが、少なくとも
が
に包含されなくて困るという心配はしなくて良くなるだろう。
もう1つの表現
実は有限体の代数的閉包はもう1つ表現方法がある。PlanetMathというウェブサイト[5]が詳しいのでこちらからいろいろ引用する。まず、 を以下のように定義する。
So we define
これに対して以下の定理が成り立つ。
("is a contained in"は"is contained in"ではないか?と思うが、気にしない方向で・・・)
証明はそこまで難しくないので、詳しくは引用先[5]を参照されたい。1つコメントしておくと、先ほど考えたような埋め込みの仕方が複数通りあるということは特に気にする必要がなく、なんでもよいので包含関係さえ成り立っていれば良さそうな感じだった。
まとめ
本稿では有限体の代数的閉包について考えた。その過程で、有限体同士の包含関係に関する微妙な問題について議論した。結論として、微妙な問題はあるものの概ね標数が同じ有限体の和集合を無限に取っていけばそれが代数閉包だということが分かった。
当初疑問に思っていたところは解消されたので、目的は達せられたと言える。ただし、Sageのドキュメントを読んでいて追加で気になったことが出てきたので、それについては次回書こうと思う。
パーセンタイルの分散って難しい
近況
久々のブログとなってしまった。最近は本職関連の勉強が忙しく、なかなか数学に手がつかなかった。転職してから1年が経過したが、現職は勉強したことがかなり業務に活かせる環境なので、勉強意欲が溢れて時間が足りない状況が続いていた。今年はなんとかバランスを取りながら、趣味の数学もやっていきたい。
Twitterの数学アカウント (@peng_theory) でつぶやきたいネタが全然出てこない時点で数学とのふれあいが足りないのは明らかなので、せめて月に1つくらいは探求すべきネタを見つけたいと思う。
それでは本題に入ろう。
Webサービスの応答性能の監視
いきなり数学らしからぬ話題になるが、Webサービスにとって応答性能は重要な指標である。もし応答性能が悪い場合、ユーザーはいつまでもロードされないブラウザの画面を見ながらストレスを溜めて、ついにはWebサービスを使うことをやめてしまうかもしれない。そこで、Webサービスの応答性能を常に監視し、応答性能の悪化に気づけるようにする監視の仕組みは重要である。
このとき、ユーザーからのリクエストに対する応答時間のデータ列に対して何らかの統計的な計算をして、その値をチェックすることになるだろう。すぐに思いつくのが平均値を使う方法である。これは全体的な傾向を掴むのにはよいかもしれないが、一方で一部のリクエストだけ異様にレスポンスが悪くなるようなケースに気づけない。このようなケースをケアしたい場合、パーセンタイルを使うことが望ましい[1]。
パーセンタイルの定義を[2]から引用する。
65パーセンタイルであれば、最小値から数えて65%に位置する値を指す。第一四分位数は25パーセンタイル、中央値は50パーセンタイル、第三四分位数は75%パーセンタイルである。
標本から計算したパーセンタイル
実際の応答時間のデータから、例えば90パーセンタイルの値を計算したとしよう。これは標本から計算した値なので、真の90パーセンタイル値とは誤差が生じると考えるべきである。では、この誤差はどのように評価されるだろうか?本稿ではこれについて考えていく。
順序統計量
パーセンタイルに近しい概念として順序統計量というものがある。順序統計量の定義については[4]が分かりやすいので引用する(ただし誤字を1つ直した)。
と記し,これらを順序統計量という.すなわち,
である.
これについて、以下の強力な定理がある[4]。
あとはパーセンタイルの値に近い順序統計量を選択すればパーセンタイルの確率密度関数が分かる。ここまで分かればパーセンタイルの分散を計算することができる。ただし、確率密度関数がなかなかに複雑なので、実際には数値計算で分散を求めることになるだろう。
実験による計算
理論的な解析は諦めてしまったわけだが、実験的にパーセンタイルの分散を求めることは可能だろう。すなわち、同じ条件で繰り返し実験を行い、各回で得られたパーセンタイルのデータ列から愚直に分散を求めようというわけである。本稿では以下の3つの確率分布からランダムにデータをサンプリングし、パーセンタイルの分散がどうなるかを調べていく。
| 確率分布 | 確率密度関数 |
|---|---|
| 一様分布 | |
| 正規分布 | |
| 指数分布 | |
ただし、実際には分散よりも標準偏差の方が応用上の使い勝手がよいため、以下では分散の代わりに標準偏差を計算している。
サンプル数による標準偏差の変化
各種パーセンタイルの標準偏差がサンプル数によりどのように変化するかを調べた。具体的には、個のサンプルを抽出してパーセンタイルを求めるという操作を、
とパーセンタイルを変えながらそれぞれ2,000回ずつ行い、パーセンタイル値の標準偏差を調べた。測定にはこちらのプログラムを使用した。
結果を以下に示す。


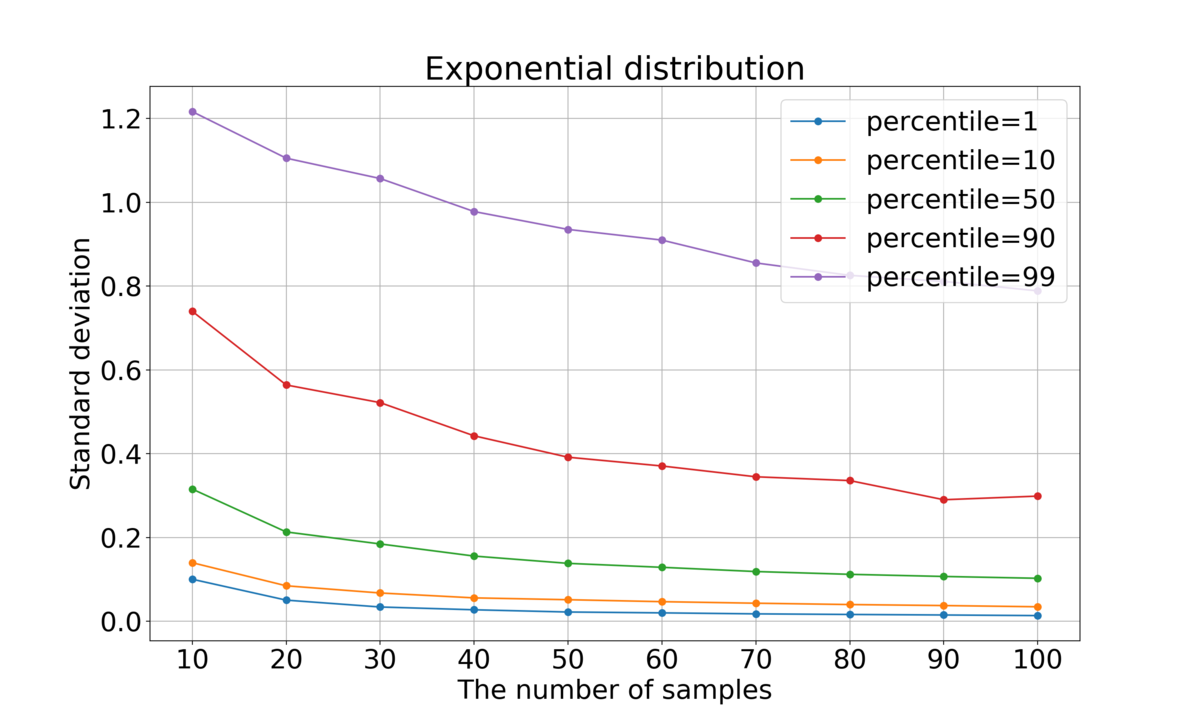
全体的にサンプル数が大きくなるほど標準偏差が小さくなっていくことが分かった。これは直観に合う結果と言ってよいだろう。
左右対称な分布(一様分布および正規分布)に対しては、当然だがパーセンタイルと
パーセンタイルはほぼ同じ値になっている。一方、指数分布の場合はそのようにはなっていない。
正規分布ではパーセンタイルが0または100に近いほど標準偏差が大きく、指数分布ではパーセンタイルが100に近いほど標準偏差が大きくなっている。これは、正規分布は正・負両方向に無限に広がっており、指数関数は正方向に無限に広がっているため、確率は低いながらどれだけでも大きい(または小さい)値を取り得るため、値が定まりづらいことに起因すると思われる。
一方、一様分布の場合はパーセンタイルが50に近づくほど標準偏差が大きかった。一様分布は両端が有限なので、端に近づくほど値が定まりやすいものと思われる。
総じて、パーセンタイルの標準偏差は分布の形状や何パーセンタイルの値を計算するかによって振る舞いが異なることが分かった。
理論値との比較
今回は既知の確率分布から人工的にデータを生成しているため、順序統計量の節で示した理論との突き合わせが可能である。面倒なのでここでは一様分布だけ詳細に確認してみる。
まず、一様分布のグラフの実データは以下のようになっていた。
| サンプル数\パーセンタイル | 1 | 10 | 50 | 90 | 99 |
|---|---|---|---|---|---|
| 10 | 0.07858139 | 0.10688424 | 0.13759072 | 0.11095673 | 0.08173355 |
| 20 | 0.04657511 | 0.07211991 | 0.10364605 | 0.07224193 | 0.04551142 |
| 30 | 0.03110218 | 0.05693209 | 0.0872053 | 0.05902791 | 0.03201352 |
| 40 | 0.02447197 | 0.05038461 | 0.07500657 | 0.0499089 | 0.02499189 |
| 50 | 0.02116183 | 0.0425881 | 0.068889 | 0.04413561 | 0.0212704 |
| 60 | 0.01853285 | 0.04200473 | 0.06251633 | 0.03993625 | 0.01942497 |
| 70 | 0.01693212 | 0.03742777 | 0.05868511 | 0.03720103 | 0.01745528 |
| 80 | 0.01563092 | 0.03405924 | 0.05434309 | 0.03480522 | 0.01503699 |
| 90 | 0.01415087 | 0.03137969 | 0.05329194 | 0.03265768 | 0.01459744 |
| 100 | 0.01352798 | 0.03021194 | 0.0493699 | 0.0302526 | 0.0134216 |
一方、順序統計量の確率密度関数から標準偏差を求める式はdesmos[5]を利用してこちらのように計算できる。サンプル数と順序
を変更可能なパラメータとして設定してあるので、いくつかピックアップして理論値を計算してみよう。
ここで一つ注意事項がある。パーセンタイルは0~100という範囲で変動するが、順序は1~
という範囲で変動する。そのため、例えば
の10パーセンタイルを計算しようとした場合、
とすると微妙に誤差が出てしまう。
正しくは以下の計算によってを求める必要がある。
厳密にはこれだとが整数にならないので、意味が判然としない計算になる。しかし、このようにして得られた
を実数も許容する拡張された順序みたいなノリで考えればまあそれらしい値にはなるだろうということで許容する。
では、いくつか値を計算して実験値と比べてみよう。
 , パーセンタイル = 1, 10, 50
, パーセンタイル = 1, 10, 50
パーセンタイル1, 10, 50に対応する順序はそれぞれ1.09, 1.9, 5.5である。先ほどのdesmosの計算式を用いて計算すると、理論的な標準偏差は0.086, 0.11, 0.14となる。一方、実験的に求めた標準偏差は0.079, 0.11, 0.14となっており、1パーセンタイル以外は同じような値になっていた。1パーセンタイルでずれが大きくなる理由については、サンプル数が小さいケースでは母分散が大きくなるため、実験により得られる不変分散が収束するために多くの試行が必要になるのかもしれない。どの実験も試行回数は2,000で固定なので、分散が本質的に大きいケースの方が不利になるのだろう。
元データの標準偏差とパーセンタイルの標準偏差の関係
次に、元データの標準偏差が変化するとパーセンタイルの標準偏差がどのように変わるかを調べた。直観的には正の相関があるものと思われるが、そこにもう少しきれいな関係性が見えないかを期待して調べてみる。ここでも一様分布のみを扱う。
まとめ
本稿ではパーセンタイルの分散について考察した。順序統計量の理論を応用し、確率密度関数や累積分布関数が既知であれば理論的にパーセンタイルの確率分布から標準偏差を計算できることについて述べた。また、実験データのように真の分布が分からない場合でも、繰り返し実験を行うことで標準偏差を求められることを示した。標準偏差が分布の形状や着目するパーセンタイルによって異なることも分かった。
ただし、実験による方法ではなかなかにたくさんの実験を行わないとパーセンタイル値が十分に収束しないため、実際には非常に大変な作業になるだろう。やはり標本平均に対する中心極限定理のように何か理論的にバシッと決まる方法が欲しいという気持ちが消えない結果となった。今後の科学の発展に期待しよう。
加えて、元データの標準偏差とパーセンタイルの標準偏差の間の関係についても調査を行った。数値計算の結果で、かつ一様分布の場合しか調べていないが、両者の間には線形関係らしきものがあることが分かって感動した。こちらについても、理論的にはどうなっているのがやはり気になるところではあるが、私の持てる実力と使える時間の制約により、今回はここまでとなった。
今回の調査の中で、私は確率・統計が結構好きだなぁと気づいた。確率論の本をずっと読破できずに積んでしまっているので、近々再チャレンジしたい。
有限体上の線形代数を探訪する ~ 双対空間編 ~
ここまで長らく有限体上の線形空間について考えてきた。本稿ではそのフィナーレとして、有限体上の線形空間の双対空間について考えてみる。
線形空間の双対空間
双対空間の定義をWikipedia[1]より引用する。
この定義では体としか言っていないので、有限体でも問題なく意味を持つ。
双対基底
次に、双対基底の定義を同じくWikipedia[1]より引用する。
を満たすものとして定義される(上付きの添字が冪を意味するものではないことに注意せよ)。
これも特別な体に限定した定義にはなっておらず、有限体でも妥当な定義である。
線形空間と双対空間の間の同型
実数体や複素数体上の線形空間の場合、有限次元であれば
と
は同型になる。これは有限次元の場合は
と
の次元が等しいことから明らかであり、有限体上の線形空間でも同様のことが言える。
具体例
ここまで確認したことを実際に計算してみよう。以下に上の3次元線形空間の双対空間や双対基底をsageを使って計算した例を示す。なお、プログラムの作成に当たってsageのドキュメント[2]のEXAMPLESを参考にした。
・計算プログラム
#!/usr/bin/env sage from sage.all import * def main(): V = FiniteRankFreeModule(GF(4), 3, name='M', start_index=1) print(f"V: {V}") basis = V.basis('e') print(f"basis: {basis}") print(f"V^*: {V.dual()}") dual_basis = basis.dual_basis() print(f"dual_basis: {dual_basis}") for i, e in enumerate(basis): for j, f in enumerate(dual_basis): print(f"f_{j+1}(e_{i+1}) = {f(e)}") if __name__ == "__main__": main()
・実行結果
% ./dual.py V: 3-dimensional vector space M over the Finite Field in z2 of size 2^2 basis: Basis (e_1,e_2,e_3) on the 3-dimensional vector space M over the Finite Field in z2 of size 2^2 V^*: Dual of the 3-dimensional vector space M over the Finite Field in z2 of size 2^2 dual_basis: Dual basis (e^1,e^2,e^3) on the 3-dimensional vector space M over the Finite Field in z2 of size 2^2 f_1(e_1) = 1 f_2(e_1) = 0 f_3(e_1) = 0 f_1(e_2) = 0 f_2(e_2) = 1 f_3(e_2) = 0 f_1(e_3) = 0 f_2(e_3) = 0 f_3(e_3) = 1
Sageでは線形空間ではなく自由加群に対して双対空間や双対基底を計算できるようだったので、そちらを使用した。実際、線形空間は(加群が久々すぎて言い切る自信がないが)自由加群の特殊なケースのはずなので、特に問題はない。
また、最後にいわゆる二重直交性を確かめてみたが、問題なく成立していることが見て取れる。
有限体上の線形代数を探訪する ~ 固有値・固有ベクトル編 ~
前回の記事では有限体上の線形空間における直交補空間について考えた。本稿ではその続きとして固有値と固有ベクトルについて考えてみる。
固有値と固有ベクトル
本[1]では実数体または複素数体のいずれかを表すということになっているが、この定義を体の視点から見るとベクトルのスカラー倍さえ定まっていれば意味を成す。したがって
を有限体としてもこの固有値・固有ベクトルの定義は妥当であると言える。
固有空間
もう一つ大切な概念として固有空間がある。これについても定義の妥当性を確認しておこう。以下に本[1]に記載されている定義を示す。
この定義も特に実数体や複素数体に固有の性質は利用していないため、有限体上の線形空間に対しても同様の定義を適用可能である。
固有空間の和
実数体や複素数体上の線形空間の場合、固有空間の和は実際には直和になる。有限体の場合も果たしてそうなるのだろうか?これを確かめるために、まず複素数体の場合の証明の概要を本[1]から抜粋する。
示すべきは、線形変換の相異なる固有値に対する固有ベクトルが線形独立になることである。相異なる固有値
に対する固有ベクトルを
とする。このとき、
が線形従属であると仮定すれば、
は線型独立だが
は線形従属であるような
が存在する。このとき、
は
(1)
と表せる。この両辺にを適用すれば
(2)
となる。式(1)の両辺にを掛けて(2)から引くと以下のようになる。
は線形独立であり、かつ
は相異なるので、
である。これより
となるが、これは
が固有ベクトルであることに矛盾する。よって仮定は誤りで、相異なる固有値に対する固有ベクトルは線形独立である。これより、固有空間の和は直和であると言える。(証明終わり)
この証明の中では複素数固有の性質は特に使われていないため、有限体でも同じように成立すると考えられる。
対角化
固有値は対角化と密接な関連がある。対角化はいつでも可能なわけではないが、有限体上の線形空間でも対角化可能となる条件は変わらないだろうか?これについて調べてみる。
まず、線形写像の表現行列が対角化可能となる条件を本[1]より引用する。
体力的に厳しいので、が固有空間の直和であれば
が対角行列で表現できることの証明だけ追ってみる。
が全て
の固有ベクトルであるとき、
に対応する固有値を
とすれば
となる。よって基底
に関する
の表現行列は
となる。(証明終わり)
この証明の中では特に実数体や複素数体固有の議論は行っていないため、有限体でも同様に成り立つ。証明をさぼったが、逆についても同様である。
ここからさらに議論を積み重ねると、ある行列が対角化可能であるためには、各固有値について固有多項式の根としての多重度と対応する固有空間の次元が一致することが必要十分条件であることが言える。これについても証明を詳細に書き記す元気がなくなってきたので断念するが、本[1]を見る限りは有限体でも同様の条件が成立すると言えそうだ。
対角化できないケースの具体例
対角化ができる条件は分かったが、実数体や複素数の場合、具体的にこの条件が満たされない状況には以下の2通りがある。
後者については体が代数閉体の場合は起こり得ないことに注意されたい。
これらのケースは有限体であっても存在する。各種具体例についてsageで計算してみた結果を以下に示す。
・計算プログラム
#!/usr/bin/env sage from sage.all import * def main(): matrixList = [] matrixList.append(matrix(GF(3), [[2, 1], [1, 2]])) matrixList.append(matrix(GF(3), [[2, 0], [0, 2]])) matrixList.append(matrix(GF(3), [[2, 1], [0, 2]])) matrixList.append(matrix(GF(2), [[1, 1], [1, 0]])) matrixList.append(matrix(GF(4), [[1, 0], [0, 1]])) for mat in matrixList: try: print(f"matrix:\n{mat}") print(f"eigen values: {mat.eigenvalues()}") print("eigen vectors(right):") for ev in mat.eigenvectors_right(): print(ev) print("eigen spaces(right):") for es in mat.eigenspaces_right(): print(es) except NotImplementedError: print("NotImplementedError occurred.") print("") if __name__ == "__main__": main()
・実行結果
./gf-eigen.py matrix: [2 1] [1 2] eigen values: [0, 1] ★多重度1の固有値が2つ eigen vectors(right): ★固有ベクトルが1つずつ (0, [ (1, 1) ], 1) (1, [ (1, 2) ], 1) eigen spaces(right): (0, Vector space of degree 2 and dimension 1 over Finite Field of size 3 User basis matrix: [1 1]) (1, Vector space of degree 2 and dimension 1 over Finite Field of size 3 User basis matrix: [1 2]) matrix: [2 0] [0 2] eigen values: [2, 2] ★多重度2の固有値が1つ eigen vectors(right): ★固有ベクトルが2つ (2, [ (1, 0), (0, 1) ], 2) eigen spaces(right): (2, Vector space of degree 2 and dimension 2 over Finite Field of size 3 User basis matrix: [1 0] [0 1]) matrix: [2 1] [0 2] eigen values: [2, 2] ★多重度2の固有値が1つ eigen vectors(right): ★固有ベクトルが1つ (2, [ (1, 0) ], 2) eigen spaces(right): (2, Vector space of degree 2 and dimension 1 over Finite Field of size 3 User basis matrix: [1 0]) matrix: [1 1] [1 0] eigen values: [z2 + 1, z2] ★2つの固有値がどちらもGF(2)の中に存在しない eigen vectors(right): ★このケースでの固有ベクトル計算はsageでは未サポート NotImplementedError occurred. matrix: [1 0] [0 1] NotImplementedError occurred. ★素数位数でない有限体について固有値計算はsageでは未サポート
やってみて分かったが、sageでは未サポートのケースがいくつかあるようだ。位数が素数でない有限体に対して固有値が計算できないのは、内部的に代数閉包を計算しており、かつそれが位数が素数でない有限体については対応していないからのようで、そのあたりのことは公式ドキュメント[3]に記載がある。
しかし、素数位数であっても固有値がベースとなる体の中に存在しないケースで固有ベクトルが計算できない理由は良く分からない。恐らく何か理論的な難しさがあるのだろう。
有限体の代数閉包
具体例を見ていく中で、いくつか私が疑問に思ったことがある。
1つ目の答えはNoである。証明は超簡単で(と言っても私は自力で思いつかなかったが)、有限体が有限個の元
から成るとする。このとき、
の根は
に含まれないので、有限体は代数閉体にはならない[2]。
では、有限体の代数閉包はどんな体になるのだろうか?軽く調べてみるといろいろ情報が出てくるが、これ単独で別の記事が書けそうな感じだったので、ここでは深入りしないでおく。これについてはまた機会があればブログに書きたいと思う。
対称行列の対角化
最後に対称行列に関して特筆すべき事項があるので、それについて紹介しよう。
実対称行列は適当な直交行列を用いて対角化可能であることが知られている。しかし、有限体の元を成分に持つ対称行列の場合は必ずしも対角化可能とは限らない[4]。
例えば、の元を成分に持つ以下のような行列を考えてみよう。
この行列の固有値は1のみで、対応する固有ベクトルはである。固有値の多重度が2で固有空間の次元が1のため、この行列は対角化できない。
なぜこうなるのかと言われると「成り立たないもんはしょうがない」ということになる(立派な反例があるので)。ただ、強いて言えば有限体の元を成分に持つ数ベクトルが成す空間では直交という概念が普通には定まらないので、そもそも直交行列の定義が怪しくなり、このような結果になっているのではないかと想像している。
有限体上の線形代数を探訪する ~ 直交補空間編 ~
前回の記事で有限体上の線形空間の定義の妥当性などを確認した。本稿ではその続きとして直交補空間について考えてみる。
なお、本稿で扱う線形空間は特に断らない限り有限次元であるとする。
ベクトルの直交性
直交補空間とは、平たく言えばある部分空間に属する全てのベクトルと直交するようなベクトル全体の集合から成るような部分空間である。そのため、直交補空間を定義するためには、まずベクトルが直交するとはどういうことかを定義しなければならない。
ベクトルが直交するというのは、内積が定められている計量線形空間であれば内積が0であることで定義される。では、有限体上の線形空間に対して内積を定義することはできるだろうか?
線形空間というのは次元さえ同じなら同型なので、最も基本的な線形空間であるに絞って考えてもバチは当たらないだろう。以前の記事でも述べたように、この空間には通常の意味での内積が定義できない。そのため、普通に考えるとベクトルの直交という概念は定義されないように思える。
双線形形式から定まる直交性
「というわけで、有限体上の線形空間には直交補空間という概念は存在しないということですね。めでたしめでたし。」としても良いのだが、どうやらここにはもう少し面白い話がありそうなことが分かった。
確かに内積を定義することはできなかったが、内積と似たような性質を持つ双線形形式を用意し、それを用いて直交性を定めるというアプローチがあるらしい。このアプローチによる直交補空間の定義をWikipedia[2]より引用する。
で定義する。同様に、右直交補空間(right orthogonal complement)も定義される。
において通常の内積のような(成分同士の積の総和を取る)演算は、内積の公理は満たさないが双線形形式にはなっている。そのため、このアプローチによりベクトルの直交性を定め、一般的な直交補空間とでも言うべきものを定義することができる。
一般的な直交補空間の性質
前述のように直交補空間を定義することはできたわけだが、相変わらず同士の内積は0になるような体たらくなので、果たして数学的に意義のあるものと言えるのだろうか?それを考えるために、このように定義した直交補空間の性質について見ていこう。
WIkipedia[2]から一般的な直交補空間が持つ性質を引用する。
- 直交補空間は、
の部分空間である;
ならば
が成立する;
の(あるいは
の)根基
は、任意の直交補空間の部分空間である;
が成立する;
が非退化かつ
が有限次元ならば、
が成立する。
ただし、は双線形形式である。
ここで、の(あるいは
の)根基とは、双線形形式
を用いて直交性を定めたときに、
の任意のベクトルと直交するようなベクトルの集合のことである[3]。根基が自明であることと双線形形式が非退化であること(これについては後述)は同値である[3]。
のベクトルに対する内積もどきは(これも後述するが)非退化であるため、有限体上の線形空間の根基は自明である。
また、が非退化であるとは、全ての
に対して
ならば、
であることを言う[4]。
のベクトルに対する内積もどきは非退化になることを以下に示す。
まず、あるが存在し、全ての
に対して
が成立すると仮定する。このとき、
の成分のうちいずれかは0ではない。これを第
成分とすると、第
成分が1、それ以外が0というベクトル
との内積は0にはならない。これは仮定に反するので、
は非退化である。
このことから、に対して
が成立すると言える。これについてはブログ[5]にも別の証明がある。
4点目について、の場合は
が成立する。これは
であること、および
から分かる[6]。
通常の直交補空間との違い
複素数体や実数体上の線形空間における通常の直交補空間の場合、は
と
との直和であるが、
では必ずしもそうはならない。例えば
について
という部分空間を考えると、
という奇妙な結果になる。
