16進数から10進数への変換を概算で求める

私はソフトウェア開発という仕事柄、日常的に16進数を扱っているのだが、16進数を10進数に変換したくなることがよくある。これはWindowsの電卓機能で簡単に実現できるためどうということはないのだが、もしこの変換を暗算で高速に行えると良いと思うことがある。

しかし、10進数と16進数というのは相性がよくない。どちらも2のべき乗であればまだ何とかなったと思うのだが、人類が10進数などというわけのわからない表記を好んで使うものだから、誤差なく簡単に変換することは不可能と思われる。ここで言う「簡単に」というのは、変換したい16進数をマウスでコピーし、Windowsの電卓アプリを開き値をペーストするよりも手軽に、という意味であると定義しておく。

そこで本稿では概算によりこの16進数から10進数への変換を簡単に行える方法について説明する。また、概算によってどれくらいの誤差が生じ得るかについても調べる。

概算の方法

概算のステップは大きく以下の2つに分けて考える。

上位桁のシンプルな数への近似
桁上げ

1点目について、概算の仕方として以下の3つの方法を考える。

ある桁以下の値を切り捨てる。
ある桁の数を7捨8入する。
ある桁の数を0, 8, 16のどれかに丸める。

上の方法ほど計算は簡単だが誤差が大きく、下の方法ほど計算は複雑だが誤差は小さくなる。

3つ目の方法について補足しておく。これは例えば0x12について、1桁目の数値が2だからこれは切り捨てて $\mathrm{0x12} \simeq \mathrm{0x10}$ とするとか、0xa7であれば間をとって8に寄せて $\mathrm{0xa7} \simeq \mathrm{0xa8}$ にするとか、そういう方法である。ただし、値がいくつであれば0, 8, 16のうちどれに丸めるかというのは選択の余地がある。

その後、0となった下位の桁の分だけ桁上げの計算を行う必要がある。例えば0x5000の場合、後ろに3つ0が並んでいるので、 $5 \times 16^3$ を計算すると、10進数への概算による変換が完了する。ただし、この計算を愚直に実行すると暗算では厳しいため、これについても概算による単純化を試みる。

対象とする16進数の大きさ

実用上、1, 2, 4, 8byteの整数値を16進数として表現することが考えられる。8byteはさすがに大きすぎて暗算では厳しそうなので、2byteの16進整数を必須の対象とし、4byteを努力目標とする。

上位桁の近似

切り捨て

前述した3つの方法のうち、もし切り捨てで話が簡単になるならそれほど嬉しいことはない。まずは楽観的にこの方針について調べてみよう。

最悪ケースでの誤差

まず、上位から3桁目以降を切り捨てた場合の誤差について考えてみる。この場合、最も切り捨てによる誤差が大きくなるのは、残された上位2桁が最小で、切り捨てられる3桁目以降が最大になる時、つまり0x10ff...fである。これの3桁目以降を切り捨てた値は0x1000...0となる。この場合の誤差は以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x1000 \cdots 0} - \mathrm{0x10ff \cdots f}|}{\mathrm{0x10ff \cdots f}} < \frac{|\mathrm{0x1000 \cdots 0} - \mathrm{0x1100 \cdots 0}|}{\mathrm{0x1000 \cdots 0}} = \frac{1}{16} = 0.0625 }$

これより、3桁目以降を切り捨てた場合の誤差は約6%以下であり、この程度であれば無視してしまってもよいだろう。よって概算を考える上では、上位2桁だけを考えればよいと言える。これは大きな収穫だ。

次に、上位から2桁目以降を切り捨てた場合の誤差について考えてみる。この場合、先ほどと同様に考えて、最も切り捨てによる誤差が大きくなるのは0x1ff...fである。これの2桁目以降を切り捨てた値は0x100...0となる。この場合の誤差は以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x100 \cdots 0} - \mathrm{0x1ff \cdots f}|}{\mathrm{0x1ff \cdots f}} < \frac{|\mathrm{0x100 \cdots 0} - \mathrm{0x200 \cdots 0}|}{\mathrm{0x1f0 \cdots 0}} = \frac{16}{31} \simeq 0.516 }$

これより、2桁目以降を切り捨てた場合の誤差は約52%以下である。さすがに2桁目の値を無視するのは誤差が大きくなりすぎるようだ。

7捨8入

上位2桁をそのまま残す必要があるとなると、暗算が苦手な私としては電卓を使いたくなる。そこで、誤差を減らすために2桁目を7捨8入することを考えてみよう。

最悪ケースでの誤差

7捨8入の場合、切り捨てる場合と切り上げる場合の誤差についてそれぞれ考える必要がある。

まず、切り捨てる場合の誤差について考えてみる。この場合、誤差が最も大きくなるのは0x17ff...fである。これの2桁目を7捨8入した値は0x1000...0となる。この場合の誤差は以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x1000 \cdots 0} - \mathrm{0x17ff \cdots f}|}{\mathrm{0x17ff \cdots f}} < \frac{|\mathrm{0x1000 \cdots 0} - \mathrm{0x1800 \cdots 0}|}{\mathrm{0x1700 \cdots 0}} = \frac{8}{23} \simeq 0.348 }$

これより、2桁目を7捨8入により切り捨てた場合の誤差は約35%以下となる。

次に、切り上げる場合の誤差について考えてみる。この場合、誤差が最も大きくなるのは0x1800...0である。これの2桁目を7捨8入した値は0x2000...0となる。この場合の誤差は以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x2000 \cdots 0} - \mathrm{0x1800 \cdots 0}|}{\mathrm{0x1800 \cdots 0}} = \frac{1}{3} \simeq 0.333 }$

これより、2桁目を7捨8入により切り捨てた場合の誤差は約33%以下となる。

切り捨てと切り上げの結果をまとめると、誤差は約35%以下と言える。先ほどよりは誤差を削減することができた。

1桁目がfの場合の切り上げ

1桁目がfの場合、2桁目を切り上げるとさらに桁上がりが発生してしまう。しかし、だからと言って特に後の計算に変化はない。このケースについては後述する具体例の中でも取り上げる。

0, 8, 16に丸める際の誤差

7捨8入によってある程度誤差を小さくできたが、1桁目の値が小さいとまだ誤差が大きい。もう少しだけ誤差を小さくするために、0, 8, 16のどれかに丸める方法を考えてみよう。

冒頭でも述べたが、この方法においては値がいくつの場合に0, 8, 16のどれに丸めるかを決めておく必要がある。できるだけ自然なルールにすることが望ましい。そこで、本稿では以下のように丸め方を決める。

上位2桁の値を2倍する。
7捨8入する。
値を2で割る。

上記手順の考え方であるが、大きい数ほど丸めの影響を受けにくいという性質に基づいている。対象となる値を2倍することで7捨8入によって混入する誤差を半分にし、その後に2で割って元のスケールに戻しているのである。このようにすることで、上位から2桁目の値が必ず0, 8のいずれかになる。また、0の場合は切り捨てされる場合と切り上げされる場合があるが、切り上げされる場合は16に丸めることに相当する。

この方法により、2桁目が0～3ならば0、4～bならば8、c～fならば16に丸められることになる。

最悪ケースでの誤差

今回は丸め先が3通りあるので、それぞれについて最悪ケースを考える必要がある。以下で順に見ていこう。

0に丸める場合

この場合、誤差が最も大きくなるのは0x13ff...fである。誤差は以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x1000 \cdots 0} - \mathrm{0x13ff \cdots f}|}{\mathrm{0x13ff \cdots f}} < \frac{|\mathrm{0x1000 \cdots 0} - \mathrm{0x1400 \cdots 0}|}{\mathrm{0x1300 \cdots 0}} = \frac{4}{19} \simeq 0.211 }$

これより、誤差が約21%以下となる。

8に丸める場合

この場合、誤差が最も大きくなるのは0x1400...0か0x1bff...fのどちらかである。誤差はそれぞれ以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x1800 \cdots 0} - \mathrm{0x1400 \cdots 0}|}{\mathrm{0x1400 \cdots 0}} = \frac{1}{5} = 0.200 }$

$\displaystyle{ \frac{|\mathrm{0x1800 \cdots 0} - \mathrm{0x1bff \cdots f}|}{\mathrm{0x1bff \cdots f}} < \frac{|\mathrm{0x1800 \cdots 0} - \mathrm{0x1c00 \cdots 0}|}{\mathrm{0x1b00 \cdots 0}} = \frac{4}{27} \simeq 0.148 }$

これより、誤差は約20%以下となる。

16に丸める場合

この場合、誤差が最も大きくなるのは0x1c00...0である。誤差は以下のように計算できる。

$\displaystyle{ \frac{|\mathrm{0x2000 \cdots 0} - \mathrm{0x1c00 \cdots 0}|}{\mathrm{0x1c00 \cdots 0}} = \frac{1}{7} \simeq 0.143 }$

これより、誤差は約14%以下となる。

結局、この方法では誤差は約21%以下に抑えられる。

ここまでのまとめ

ここまでの議論をまとめておく。16進数から10進数への変換を概算で求める際、上位から3桁目以降は無視してよいが、2桁目は無視できない。

最上位桁がある程度大きければ上位から2桁目以降を切り捨てても問題ないが、7捨8入くらいであれば暗算でも苦労なく行えるので、あまり考えずに7捨8入してしまうのがよいだろう。

最上位桁がある程度小さい場合、0, 8, 16にまとめる方法によって誤差を抑えることができる。しかし、8に丸める場合は上位2桁が残ってしまう。これだとこの後の桁上げの計算が煩雑になるため、このケースは素直に電卓を使った方が速いだろう。もしくは、35%程度の誤差が許容できるのであれば7捨8入してもよい。

桁上げの計算

これまで上位2桁の誤差にだけ着目して議論してきたが、ここからは桁上げの概算方法について考えてみよう。

今、7捨8入によって値は必ず0xz00...0という形になっている。zには適当な値が入る。zの後に続く0の数を $n$ とすると、10進数としての値は以下のようになる。

$\displaystyle{ z_{10} \times 16^n = z_{10} \times 2^{4n} }$

ただし、 $z_{10}$ はzを10進数で表した数を意味する。ここで、右辺を暗算で正確に計算しようとすると、場合によってはかなり厳しいことが分かる。例えばz = d, n = 3の場合を考えると、 $13 \times 2^{12}$ という計算を実行する必要があり、大変面倒くさい。

そこで、以下の4つの近似によって計算を簡略化する。

$z_{10}$ を偶数に丸める。
$2^{10} \simeq 1000$ と置き換える。
$2^{9} \simeq 500$ と置き換える。
$2^{5} \simeq 30$ と置き換える。

2つ目から4つ目は古典的な方法なので説明を割愛し、1つ目についてのみ説明する。

1桁目の16進数を偶数に丸める

先ほどの計算例でz = cとすると、 $12 \times 2^{12}$ を計算することになる。12は偶数、しかも4の倍数なので、実際に計算を開始する前に $3 \times 2^{14}$ という形に変換できる。ここまでくれば、あとは $3 \times 2^4 \times 1000 = 48000$ と近似計算できる。実際、 $\mathrm{0xc000} = 49152$ なので、これはそこまで外していない。

つまり、偶数の場合は計算が幾分かやりやすくなるのである。そこで、zが奇数の場合は1足すか引くかして、偶数に丸めてしまえばよい。ただし、 $z_{10}$ が1桁の奇数の場合、値が1変わるとそれだけで10%以上の誤差が生じる。1桁の場合はそもそもそこまで計算が大変でもないので、この近似は $z_{10}$ が2桁の場合にのみ実施する。

あと決めることは奇数に対して1足すか引くかである。対象となる奇数は11, 13, 15である。折角なら4の倍数に丸めた方が後の計算が楽になるので、これらはそれぞれ12, 12, 16に丸めることにする。

誤差の評価

桁上げ、および11, 13, 15の偶数への丸め誤差について考える。まず、 $2^{5}$ , $2^{9}$ , $2^{10}$ を30, 500, 1000と近似する際の誤差はそれぞれ以下のようになる。

$\displaystyle{ \frac{|30 - 32|}{32} = \frac{1}{16} = 0.0625 }$

$\displaystyle{ \frac{|500 - 512|}{512} = \frac{3}{128} = 0.0234 }$

$\displaystyle{ \frac{|1000 - 1024|}{1024} = \frac{3}{128} \simeq 0.0234 }$

11, 13, 15の偶数への丸めについては11のケースで一番誤差が大きくなるので、11についてのみ誤差を計算する。

$\displaystyle{ \frac{|12 - 11|}{11} = \frac{1}{11} \simeq 0.0909 }$

これらの近似は場合によって実施したり実施しなかったりするので、上記の誤差は近似を行った場合にのみ混入する。

手順まとめ

以上の議論をもとに、最終的な手順をまとめておく。

上位から2桁目を7捨8入する。
1桁目の値を10進数に変換したとき、11, 13, 15であればそれぞれ12, 12, 16に置き換える。
1桁目の値の素因数のうち2の個数を $m$ とし、それ以外の素因数の積を $g$ とする。また、2桁目以降の桁数を $n$ とする。この時、上記ステップまでの変換で得られた数を $g \times 2^{m+4n}$ という形で表せる。
$10 \le m+4n$ であれば $2^{10}$ の素因数を1000で置き換える。さらに残った指数部が9以上または5以上であれば $2^9$ , $2^5$ をそれぞれ500, 30で置き換える。
あとは素直に計算する。

計算全体の誤差

ここまで計算の各種ステップにおける誤差については都度説明してきた。実際にはそれらがすべて積みあがったものが計算全体の誤差となる。本当は誤差についてはいろいろと理論があるようだが、厳密に誤差を評価することは今の私の実力では難しいため、厳しめに評価して単純に誤差を足し合わせるのが安全だろう。

ただし、一番誤差が大きくなるポテンシャルがある7捨8入で実際に誤差が大きくなるのは1桁目が小さいときである。この時は1桁目を偶数に置き換えることはしないため、これらの誤差が同時にのしかかることはない。結局、1桁目が1のときにかかる約35%の誤差と桁上げの誤差数%を合わせた40%程度の誤差が最大と考えられる。

具体例

いくつか具体例を示しておく。

0x750e

正確な値は29966である。

上位から2桁目を7捨8入すると0x7000となる。最上位桁が10進で1桁なので、置き換えは必要ない。すると、 $\mathrm{0x7000} = 7 \times 2^{12}$ となる。 $2^{10}$ を1000で置き換えると $7 \times 4 \times 1000$ となる。これを計算して28000を得る。

0xc9af

正確な値は51631である。

上位から2桁目を7捨8入すると0xd000となる。0xd = 13なので12 = 0xcに置き換える。すると、 $\mathrm{0xc000} = 3 \times 2^{2 + 12} = 3 \times 2^{14}$ となる。 $2^{10}$ を1000で置き換えると $3 \times 16 \times 1000$ となる。これを計算して48000を得る。

0xeb0abc43

正確な値は3943349315である。

上位から2桁目を7捨8入すると0xf0000000となる。0xf = 15なので16 = 0x10に置き換える。すると、 $\mathrm{0x100000000} = 1 \times 2^{32}$ となる。 $2^{10}$ を1000で置き換えると $4 \times 1000 \times 1000 \times 1000$ となる。これを計算して4000000000を得る。

0xfa000000

正確な値は4194304000である。

上位から2桁目を7捨8入すると0x100000000となる。もともと1桁目がfなので、2桁目を切り上げるとさらに桁上がりが発生している点に注意されたい。最上位桁が10進で1桁なので、置き換えは必要ない。すると、 $\mathrm{0x100000000} = 1 \times 2^{32}$ となる。 $2^{10}$ を1000で置き換えると $4 \times 1000 \times 1000 \times 1000$ となる。これを計算して4000000000を得る。

誤差の推移

最後に、もっと多くの具体例について、それぞれ誤差がどうなるかを見てみよう。

16進数	10進数	近似値	誤差[%]
0x1000	4096	4000	2.34
0x1700	5888	4000	32.1
0x1e00	7680	8000	4.17
0x2500	9472	8000	15.5
0x2c00	11264	12000	6.53
0x3300	13056	12000	8.09
0x3a00	14848	16000	7.76
0x4100	16640	16000	3.85
0x4800	18432	20000	8.51
0x4f00	20224	20000	1.11
0x5600	22016	20000	9.16
0x5d00	23808	24000	0.80
0x6400	25600	24000	6.25
0x6b00	27392	28000	2.22
0x7200	29184	28000	4.06
0x7900	30976	32000	3.31
0x8000	32768	32000	2.34
0x8700	34560	32000	7.41
0x8e00	36352	36000	0.968
0x9500	38144	36000	5.62
0x9c00	39936	40000	0.160
0xa300	41728	40000	4.14
0xaa00	43520	48000	10.1
0xb100	45312	48000	5.93
0xb800	47104	48000	1.90
0xbf00	48896	48000	1.83
0xc600	50688	48000	5.30
0xcd00	52480	48000	8.54
0xd400	54272	48000	11.6
0xdb00	56064	56000	0.114
0xe200	57856	56000	3.21
0xe900	59648	60000	0.590
0xf000	61440	60000	2.34
0xf700	63232	60000	5.11
0xfe00	65024	60000	7.73

グラフも載せておく。

f:id:peng225:20200101225305p:plain

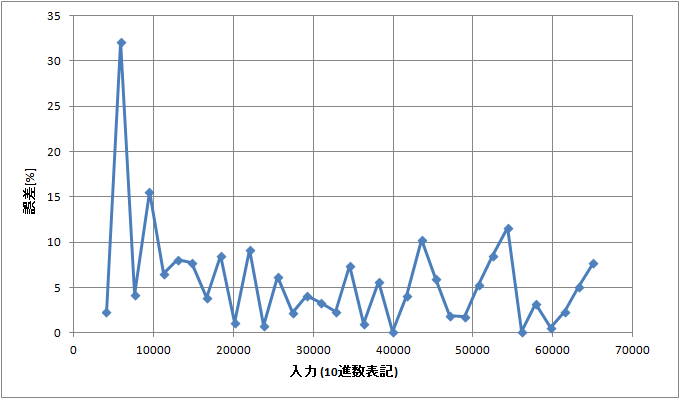
入力が小さいところで誤差が大きいのは7捨8入による影響である。入力が大きいところでも小さいピークがみられるのは、奇数を偶数に丸めている影響である。上記はあくまでサンプリングを行った上でのプロットであるため確かなことは言えないが、1桁目が3以上であればある程度誤差を気にせず概算を行うことができそうだ。

まとめ

本稿では16進数の10進数への変換を概算によって高速に行う方法について述べた。正直、期待したほど良い結果は得られなかったが、誤差の振る舞いについて理解していれば何とか使えそうな方法を編み出すことができた。やはり世の中に確立された方法がないということは、それだけ難しいテーマだということなのだろう。