パーセンタイルの分散って難しい

近況

久々のブログとなってしまった。最近は本職関連の勉強が忙しく、なかなか数学に手がつかなかった。転職してから1年が経過したが、現職は勉強したことがかなり業務に活かせる環境なので、勉強意欲が溢れて時間が足りない状況が続いていた。今年はなんとかバランスを取りながら、趣味の数学もやっていきたい。

Twitterの数学アカウント (@peng_theory) でつぶやきたいネタが全然出てこない時点で数学とのふれあいが足りないのは明らかなので、せめて月に1つくらいは探求すべきネタを見つけたいと思う。

それでは本題に入ろう。

Webサービスの応答性能の監視

いきなり数学らしからぬ話題になるが、Webサービスにとって応答性能は重要な指標である。もし応答性能が悪い場合、ユーザーはいつまでもロードされないブラウザの画面を見ながらストレスを溜めて、ついにはWebサービスを使うことをやめてしまうかもしれない。そこで、Webサービスの応答性能を常に監視し、応答性能の悪化に気づけるようにする監視の仕組みは重要である。

このとき、ユーザーからのリクエストに対する応答時間のデータ列に対して何らかの統計的な計算をして、その値をチェックすることになるだろう。すぐに思いつくのが平均値を使う方法である。これは全体的な傾向を掴むのにはよいかもしれないが、一方で一部のリクエストだけ異様にレスポンスが悪くなるようなケースに気づけない。このようなケースをケアしたい場合、パーセンタイルを使うことが望ましい[1]。

パーセンタイルの定義を[2]から引用する。

パーセンタイル

データを小さい順に並べたとき、初めから数えて全体の $100 \alpha$ %に位置する値を $100 \alpha$ パーセンタイルと言う( $0 \le \alpha \le 1$ )。

65パーセンタイルであれば、最小値から数えて65%に位置する値を指す。第一四分位数は25パーセンタイル、中央値は50パーセンタイル、第三四分位数は75%パーセンタイルである。

標本から計算したパーセンタイル

実際の応答時間のデータから、例えば90パーセンタイルの値を計算したとしよう。これは標本から計算した値なので、真の90パーセンタイル値とは誤差が生じると考えるべきである。では、この誤差はどのように評価されるだろうか？本稿ではこれについて考えていく。

標本平均の場合

ちなみに、標本平均の場合は議論がずっと簡単になる。というのも、中心極限定理により、元データが従う確率分布によらずサンプル数 $n$ が増えていけば標本平均は近似的に正規分布に従い、その分散は $\frac{\sigma^2}{n}$ ( $\sigma^2$ は元データの母分散) となるためである[3]。実際には母分散は分からないことが多いが、そこは不偏分散で代用してもよいだろう。

順序統計量

パーセンタイルに近しい概念として順序統計量というものがある。順序統計量の定義については[4]が分かりやすいので引用する（ただし誤字を1つ直した）。

順序統計量

$X_1, X_2, \ldots, X_n$ をランダム標本としたとき，これを小さい順に並べかえたものを
$\displaystyle{ X_{(1)}, X_{(2)}, \ldots, X_{(n)} }$
と記し，これらを順序統計量という．すなわち，
$\displaystyle{ \begin{eqnarray} X_{(1)} &=& \min \{X_1, X_2, ... , X_n \}, \\ X_{(2)} &=& X_1, X_2, ..., X_n の中で 2 番目に小さいもの, \\ &.& \\ &.& \\ &.& \\ X_{(n)} &=& \max \{X_1, X_2, ..., X_n \}, \\ \end{eqnarray} }$
である．

これについて、以下の強力な定理がある[4]。

順序統計量の確率密度関数

$X_1, X_2, \ldots, X_n$ を分布関数 $F_X(x)$ と確率密度関数 $f_X(x)$ をもつ連続型分布からの標本の大きさが $n$ のランダム標本とする． $X_{(1)}, X_{(2)}, \ldots, X_{(n)}$ を標本の順序統計量としたとき， $X_{(j)}, j = 1, 2, . . . , n,$ の確率密度関数は
$\displaystyle{ f_{X_{(j)}} (x) = \frac{n!}{(j − 1)!(n − j)!} f_X (x)[F_X(x)]^{j−1}[1 − F_X(x)]^{n−j} }$
となる．

あとは $100 \alpha$ パーセンタイルの値に近い順序統計量を選択すればパーセンタイルの確率密度関数が分かる。ここまで分かればパーセンタイルの分散を計算することができる。ただし、確率密度関数がなかなかに複雑なので、実際には数値計算で分散を求めることになるだろう。

確率分布が不明な場合

上記の定理は非常に強力である一方、分布関数 $F_X(x)$ と確率密度関数 $f_X(x)$ が既知であることが前提となる。冒頭で述べたような実際のWebシステムの応答性能のようなデータについては、分布関数も確率密度関数も分かりようがない。そのため、この定理をそのまま適用することはできない。

実験による計算

理論的な解析は諦めてしまったわけだが、実験的にパーセンタイルの分散を求めることは可能だろう。すなわち、同じ条件で繰り返し実験を行い、各回で得られたパーセンタイルのデータ列から愚直に分散を求めようというわけである。本稿では以下の3つの確率分布からランダムにデータをサンプリングし、パーセンタイルの分散がどうなるかを調べていく。

確率分布	確率密度関数
一様分布	$1 (0 \le x \le 1), 0 (otherwise)$
正規分布	$N(0, 1)$
指数分布	$\exp(-x) (0 \le x), 0 (otherwise)$

ただし、実際には分散よりも標準偏差の方が応用上の使い勝手がよいため、以下では分散の代わりに標準偏差を計算している。

サンプル数による標準偏差の変化

各種パーセンタイルの標準偏差がサンプル数によりどのように変化するかを調べた。具体的には、 $n$ 個のサンプルを抽出してパーセンタイルを求めるという操作を、 $n$ とパーセンタイルを変えながらそれぞれ2,000回ずつ行い、パーセンタイル値の標準偏差を調べた。測定にはこちらのプログラムを使用した。

結果を以下に示す。

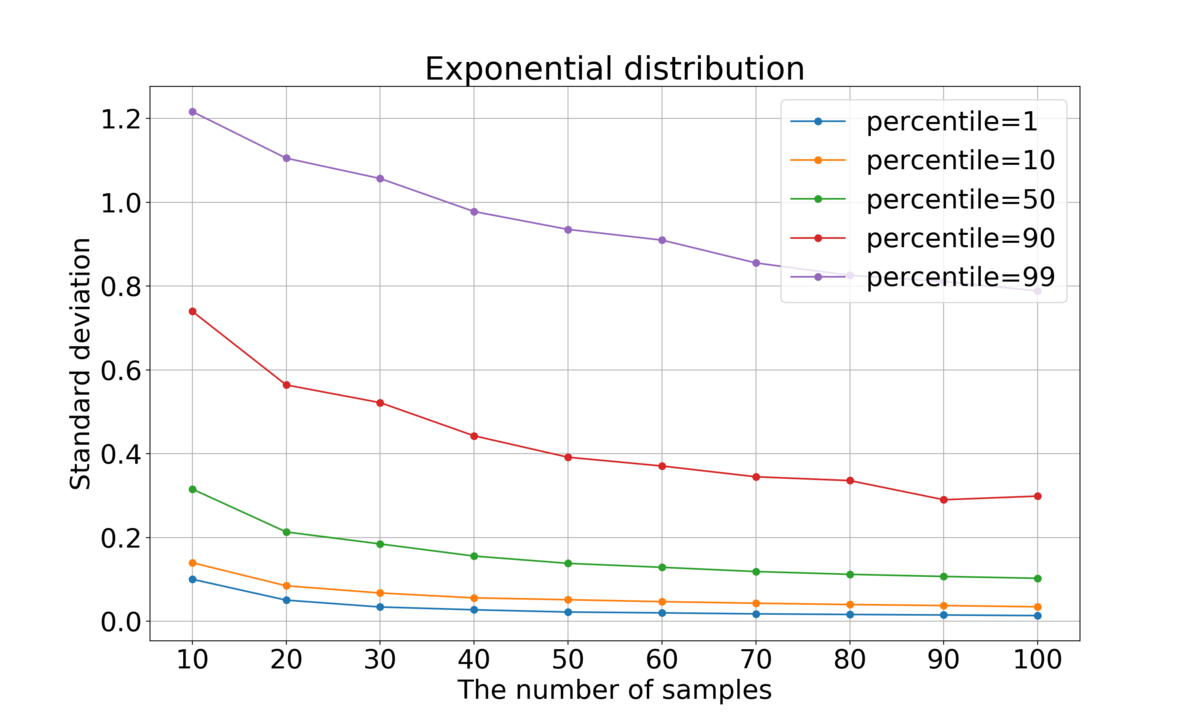
全体的にサンプル数が大きくなるほど標準偏差が小さくなっていくことが分かった。これは直観に合う結果と言ってよいだろう。

左右対称な分布（一様分布および正規分布）に対しては、当然だが $100\alpha$ パーセンタイルと $100(1-\alpha)$ パーセンタイルはほぼ同じ値になっている。一方、指数分布の場合はそのようにはなっていない。

正規分布ではパーセンタイルが0または100に近いほど標準偏差が大きく、指数分布ではパーセンタイルが100に近いほど標準偏差が大きくなっている。これは、正規分布は正・負両方向に無限に広がっており、指数関数は正方向に無限に広がっているため、確率は低いながらどれだけでも大きい（または小さい）値を取り得るため、値が定まりづらいことに起因すると思われる。

一方、一様分布の場合はパーセンタイルが50に近づくほど標準偏差が大きかった。一様分布は両端が有限なので、端に近づくほど値が定まりやすいものと思われる。

総じて、パーセンタイルの標準偏差は分布の形状や何パーセンタイルの値を計算するかによって振る舞いが異なることが分かった。

理論値との比較

今回は既知の確率分布から人工的にデータを生成しているため、順序統計量の節で示した理論との突き合わせが可能である。面倒なのでここでは一様分布だけ詳細に確認してみる。

まず、一様分布のグラフの実データは以下のようになっていた。

サンプル数\パーセンタイル	1	10	50	90	99
10	0.07858139	0.10688424	0.13759072	0.11095673	0.08173355
20	0.04657511	0.07211991	0.10364605	0.07224193	0.04551142
30	0.03110218	0.05693209	0.0872053	0.05902791	0.03201352
40	0.02447197	0.05038461	0.07500657	0.0499089	0.02499189
50	0.02116183	0.0425881	0.068889	0.04413561	0.0212704
60	0.01853285	0.04200473	0.06251633	0.03993625	0.01942497
70	0.01693212	0.03742777	0.05868511	0.03720103	0.01745528
80	0.01563092	0.03405924	0.05434309	0.03480522	0.01503699
90	0.01415087	0.03137969	0.05329194	0.03265768	0.01459744
100	0.01352798	0.03021194	0.0493699	0.0302526	0.0134216

一方、順序統計量の確率密度関数から標準偏差を求める式はdesmos[5]を利用してこちらのように計算できる。サンプル数 $n$ と順序 $j$ を変更可能なパラメータとして設定してあるので、いくつかピックアップして理論値を計算してみよう。

ここで一つ注意事項がある。パーセンタイルは0～100という範囲で変動するが、順序 $j$ は1～ $n$ という範囲で変動する。そのため、例えば $n = 100$ の10パーセンタイルを計算しようとした場合、 $j=10$ とすると微妙に誤差が出てしまう。

正しくは以下の計算によって $j$ を求める必要がある。

$\displaystyle{ j = 1 + \alpha (n-1) }$

厳密にはこれだと $j$ が整数にならないので、意味が判然としない計算になる。しかし、このようにして得られた $j$ を実数も許容する拡張された順序みたいなノリで考えればまあそれらしい値にはなるだろうということで許容する。

では、いくつか値を計算して実験値と比べてみよう。

$n=10$ , パーセンタイル = 1, 10, 50

パーセンタイル1, 10, 50に対応する順序 $j$ はそれぞれ1.09, 1.9, 5.5である。先ほどのdesmosの計算式を用いて計算すると、理論的な標準偏差は0.086, 0.11, 0.14となる。一方、実験的に求めた標準偏差は0.079, 0.11, 0.14となっており、1パーセンタイル以外は同じような値になっていた。1パーセンタイルでずれが大きくなる理由については、サンプル数が小さいケースでは母分散が大きくなるため、実験により得られる不変分散が収束するために多くの試行が必要になるのかもしれない。どの実験も試行回数は2,000で固定なので、分散が本質的に大きいケースの方が不利になるのだろう。

$n=100$ , パーセンタイル = 50, 90, 99

パーセンタイル50, 90, 99に対応する順序 $j$ はそれぞれ50.5, 90.1, 99.01である。先ほどのdesmosの計算式を用いて計算すると、理論的な標準偏差は0.050, 0.031, 0.014となる。一方、実験的に求めた標準偏差は0.050, 0.030, 0.013となっており、こちらもだいたい同じような値になっていると言えそうだ。

以上により、理論的な解析と実験結果が概ね一致することが分かった。

元データの標準偏差とパーセンタイルの標準偏差の関係

次に、元データの標準偏差が変化するとパーセンタイルの標準偏差がどのように変わるかを調べた。直観的には正の相関があるものと思われるが、そこにもう少しきれいな関係性が見えないかを期待して調べてみる。ここでも一様分布のみを扱う。

解析的なアプローチ

パーセンタイルの標準偏差を一様分布の標準偏差 $\sigma$ の関数として表すことができれば両者の関係が分かる。そのために、まず順序統計量の確率密度関数を $\sigma$ の関数として表したい。

標準偏差が $\sigma$ となる一様分布の確率密度関数のうち、値が正となる区間が0から始まるものは以下のようになる。

$\displaystyle{ f(x) = \begin{cases} \frac{1}{2\sqrt{3} \sigma} & (0 \le x \le 2\sqrt{3} \sigma) \\ 0 & (otherwise) \end{cases} }$

これより、順序統計量 $X_{(j)}$ の確率密度関数は以下のようになる。

$\displaystyle{ f_{X_{(j)}} (x) = \frac{n!}{\left(2\sqrt{3} \sigma \right)^n (j − 1)!(n − j)!} x^{j−1} \left(2\sqrt{3} \sigma − x \right)^{n−j} }$

ここから平均値を求めて分散を求めて・・・と進めていけば最終的には順序統計量の標準偏差を $\sigma$ の関数として表すことができるはずだが、これは死ぬほど骨が折れる計算になる。少なくとも私は諦めた。

数値計算的なアプローチ

というわけで、またもやdesmosを使用してグラフをこのように書いてみた。ここで、横軸（計算式における変数 $x$ ）は $\sigma$ 、縦軸は順序 $j$ の順序統計量の標準偏差を表す。計算が激重なので辛抱強く待つ必要があるが、なんと美しい一次関数らしきものが現れたではないか！私は感動のあまり鳥肌が立った。

実は、元データの標準偏差と標本平均の標準偏差の間には線形関係があるので、パーセンタイルにも似たような線形関係が現れないかとこっそり期待していたのだが、ここまでうまくいくとは驚いた。

ただし、これはあくまで数値計算の結果であり、本当に一次関数になっているかは依然として不明である点は注意されたい。

まとめ

本稿ではパーセンタイルの分散について考察した。順序統計量の理論を応用し、確率密度関数や累積分布関数が既知であれば理論的にパーセンタイルの確率分布から標準偏差を計算できることについて述べた。また、実験データのように真の分布が分からない場合でも、繰り返し実験を行うことで標準偏差を求められることを示した。標準偏差が分布の形状や着目するパーセンタイルによって異なることも分かった。

ただし、実験による方法ではなかなかにたくさんの実験を行わないとパーセンタイル値が十分に収束しないため、実際には非常に大変な作業になるだろう。やはり標本平均に対する中心極限定理のように何か理論的にバシッと決まる方法が欲しいという気持ちが消えない結果となった。今後の科学の発展に期待しよう。

加えて、元データの標準偏差とパーセンタイルの標準偏差の間の関係についても調査を行った。数値計算の結果で、かつ一様分布の場合しか調べていないが、両者の間には線形関係らしきものがあることが分かって感動した。こちらについても、理論的にはどうなっているのがやはり気になるところではあるが、私の持てる実力と使える時間の制約により、今回はここまでとなった。

今回の調査の中で、私は確率・統計が結構好きだなぁと気づいた。確率論の本をずっと読破できずに積んでしまっているので、近々再チャレンジしたい。

参考

[1] Google - Site Reliability Engineering
[2] パーセンタイル | 統計用語集 | 統計WEB
[3] 中心極限定理 - Wikipedia
[4] https://mcm-www.jwu.ac.jp/~konno/pdf/statha18.pdf
[5] Desmos | Beautiful, Free Math